Transformarea graficelor de funcții logaritmice complexe. Transformarea graficelor funcţiilor elementare
Functie exponentiala este o generalizare a produsului a n numere egale cu a:
y (n) = a n = a·a·a···a,
la mulțimea numerelor reale x:
y (x) = ax.
Aici a este un număr real fix, care este numit baza functiei exponentiale.
Se mai numește și o funcție exponențială cu baza a exponent la baza a.
Generalizarea se realizează după cum urmează.
Pentru natural x = 1, 2, 3,...
, funcția exponențială este produsul x factori:
.
Mai mult, are proprietăți (1,5-8) (), care decurg din regulile de înmulțire a numerelor. Pentru valorile zero și negative ale numerelor întregi, funcția exponențială este determinată folosind formulele (1.9-10). Pentru valorile fracționale x = m/n numere raționale, , se determină prin formula (1.11). Pentru real, funcția exponențială este definită ca limita a secvenței:
,
unde este o succesiune arbitrară de numere raționale care converg către x: .
Cu această definiție, funcția exponențială este definită pentru toate , și satisface proprietățile (1.5-8), ca pentru x natural.
O formulare matematică riguroasă a definiției unei funcții exponențiale și demonstrarea proprietăților acesteia este dată la pagina „Definiția și demonstrarea proprietăților unei funcții exponențiale”.
Proprietățile funcției exponențiale
Funcția exponențială y = a x are următoarele proprietăți pe mulțimea numerelor reale ():
(1.1)
definit si continuu, pentru , pentru toti ;
(1.2)
pentru un ≠ 1
are multe semnificații;
(1.3)
strict crește la , scade strict la ,
este constantă la ;
(1.4)
la ;
la ;
(1.5)
;
(1.6)
;
(1.7)
;
(1.8)
;
(1.9)
;
(1.10)
;
(1.11)
,
.
Alte formule utile.
.
Formula pentru conversia într-o funcție exponențială cu o bază de exponent diferită:
Când b = e, obținem expresia funcției exponențiale prin exponențială:
Valori private
, , , , .
Figura prezintă grafice ale funcției exponențiale
y (x) = ax
pentru patru valori baze de grad: a = 2
, a = 8
, a = 1/2
și a = 1/8
. Se vede că pentru un > 1
funcţia exponenţială creşte monoton. Cu cât baza gradului a este mai mare, cu atât mai mult crestere puternica. La 0
< a < 1
funcţia exponenţială scade monoton. Cu cât exponentul a este mai mic, cu atât scăderea este mai puternică.
Urcând, coborând
Funcția exponențială pentru este strict monotonă și, prin urmare, nu are extreme. Principalele sale proprietăți sunt prezentate în tabel.
| y = a x , a > 1 | y = ax, 0 < a < 1 | |
| Domeniu | - ∞ < x < + ∞ | - ∞ < x < + ∞ |
| Gama de valori | 0 < y < + ∞ | 0 < y < + ∞ |
| Monoton | crește monoton | scade monoton |
| Zerouri, y = 0 | Nu | Nu |
| Interceptarea punctelor cu axa ordonatelor, x = 0 | y= 1 | y= 1 |
| + ∞ | 0 | |
| 0 | + ∞ |
Funcție inversă
Inversa unei funcții exponențiale cu baza a este logaritmul cu baza a.
Daca atunci
.
Daca atunci
.
Diferențierea unei funcții exponențiale
Pentru a diferenția o funcție exponențială, baza acesteia trebuie redusă la numărul e, aplicați tabelul derivatelor și regula de diferențiere a unei funcții complexe.
Pentru a face acest lucru, trebuie să utilizați proprietatea logaritmilor
și formula din tabelul derivatelor:
.
Să fie dată o funcție exponențială:
.
O aducem la baza e:
Să aplicăm regula de diferențiere a funcțiilor complexe. Pentru a face acest lucru, introduceți variabila
Apoi
Din tabelul derivatelor avem (înlocuiește variabila x cu z):
.
Deoarece este o constantă, derivata lui z față de x este egală cu
.
Conform regulii de diferențiere a unei funcții complexe:
.
Derivată a unei funcții exponențiale
.
Derivată de ordin al n-lea:
.
Formule derivate > > >
Un exemplu de diferențiere a unei funcții exponențiale
Aflați derivata unei funcții
y= 3 5 x
Soluţie
Să exprimăm baza funcției exponențiale prin numărul e.
3 = e ln 3
Apoi
.
Introduceți o variabilă
.
Apoi
Din tabelul derivatelor găsim:
.
Deoarece 5ln 3 este o constantă, atunci derivata lui z față de x este egală cu:
.
Conform regulii de diferențiere a unei funcții complexe, avem:
.
Răspuns
Integral
Expresii folosind numere complexe
Luați în considerare funcția număr complex z:
f (z) = a z
unde z = x + iy; i 2 = - 1
.
Să exprimăm constanta complexă a în termeni de modul r și argument φ:
a = r e i φ
Apoi
.
Argumentul φ nu este definit în mod unic. ÎN vedere generala
φ = φ 0 + 2 πn,
unde n este un număr întreg. Prin urmare, funcția f (z) nici nu este clar. Semnificația sa principală este adesea luată în considerare
.
Extinderea seriei
.
Referinte:
ÎN. Bronstein, K.A. Semendyaev, Manual de matematică pentru ingineri și studenți, „Lan”, 2009.
În funcție de condițiile proceselor fizice, unele cantități iau valori constante și se numesc constante, altele se modifică în anumite condiții și se numesc variabile.
Un studiu atent al mediului arată că mărimi fizice dependente unele de altele, adică modificarea unor cantități atrage după sine o modificare a altora.
Analiza matematică se ocupă cu studiul relațiilor cantitative dintre cantități care se variază reciproc, făcând abstracție de sensul fizic specific. Unul dintre conceptele de bază ale analizei matematice este conceptul de funcție.
Luați în considerare elementele mulțimii și elementele mulțimii  (Fig. 3.1).
(Fig. 3.1).

Dacă între elementele mulţimilor se stabileşte o oarecare corespondenţă  Și
Și  sub forma unei reguli
sub forma unei reguli  , apoi notează că funcția este definită
, apoi notează că funcția este definită  .
.
Definiție
3.1.
Corespondenţă  , care se asociază cu fiecare element
, care se asociază cu fiecare element  nu set gol
nu set gol  un element bine definit
un element bine definit  nu set gol
nu set gol  , numită funcție sau mapare
, numită funcție sau mapare  V
V  .
.
Afișare simbolică  V
V  se scrie astfel:
se scrie astfel:
 .
.
În același timp, mulți  se numeste domeniul de definitie al functiei si se noteaza
se numeste domeniul de definitie al functiei si se noteaza  .
.
La rândul lor, mulți  se numește intervalul de valori ale funcției și se notează
se numește intervalul de valori ale funcției și se notează  .
.
În plus, trebuie remarcat faptul că elementele setului  se numesc variabile independente, elementele multimii
se numesc variabile independente, elementele multimii  se numesc variabile dependente.
se numesc variabile dependente.
Metode pentru specificarea unei funcții
Funcția poate fi specificată în următoarele moduri principale: tabelar, grafic, analitic.
Dacă, pe baza datelor experimentale, sunt compilate tabele care conțin valorile funcției și valorile argumentelor corespunzătoare, atunci această metodă de specificare a funcției se numește tabulară.
În același timp, dacă unele studii ale rezultatului experimental sunt afișate pe un înregistrator (osciloscop, înregistrator etc.), atunci se observă că funcția este specificată grafic.
Cel mai comun este modul analitic de specificare a unei funcții, adică. o metodă în care o variabilă independentă și dependentă este legată folosind o formulă. În acest caz, domeniul de definire a funcției joacă un rol semnificativ:
diferite, deși sunt date de aceleași relații analitice.
Dacă specificați doar formula funcției  , atunci considerăm că domeniul de definire al acestei funcții coincide cu mulțimea acelor valori ale variabilei
, atunci considerăm că domeniul de definire al acestei funcții coincide cu mulțimea acelor valori ale variabilei  , pentru care expresia
, pentru care expresia  are sensul. În acest sens, problema găsirii domeniului de definire a unei funcții joacă un rol deosebit.
are sensul. În acest sens, problema găsirii domeniului de definire a unei funcții joacă un rol deosebit.
Sarcină 3.1. Găsiți domeniul unei funcții

Soluţie
Primul termen ia valori reale când  , iar al doilea la. Astfel, pentru a găsi domeniul de definiție al unei funcții date, este necesar să se rezolve sistemul de inegalități:
, iar al doilea la. Astfel, pentru a găsi domeniul de definiție al unei funcții date, este necesar să se rezolve sistemul de inegalități:

Ca urmare, soluția pentru un astfel de sistem este . Prin urmare, domeniul de definire al funcției este segmentul  .
.
Cele mai simple transformări ale graficelor de funcții
Construcția graficelor de funcții poate fi simplificată semnificativ dacă utilizați graficele binecunoscute ale funcțiilor elementare de bază. Următoarele funcții sunt numite funcții elementare principale:
1) funcția de putere  Unde
Unde  ;
;
2) funcția exponențială  Unde
Unde 
 Și
Și  ;
;
3) funcția logaritmică  , Unde
, Unde  - orice număr pozitiv, altul decât unul:
- orice număr pozitiv, altul decât unul:  Și
Și  ;
;
4) funcții trigonometrice 



 ;
;
 .
.
5) funcții trigonometrice inverse  ;
; ;
;
 ;
;
 .
.
Funcțiile elementare sunt funcții care sunt obținute din funcții elementare de bază folosind patru operații aritmetice și suprapoziții aplicate de un număr finit de ori.
Transformările geometrice simple fac, de asemenea, posibilă simplificarea procesului de construire a unui grafic de funcții. Aceste transformări se bazează pe următoarele afirmații:
Graficul funcției y=f(x+a) este graficul y=f(x), deplasat (pentru a >0 la stânga, pentru a< 0 вправо) на |a| единиц параллельно осиOx.
Graficul funcției y=f(x) +b este graficul lui y=f(x), deplasat (la b>0 în sus, la b< 0 вниз) на |b| единиц параллельно осиOy.
Graficul funcției y = mf(x) (m0) este graficul lui y = f(x), întins (la m>1) de m ori sau comprimat (la 0 Graficul funcției y = f(kx) este graficul lui y = f(x), comprimat (pentru k >1) de k ori sau întins (pentru 0< k < 1) вдоль оси Ox. При –< k < 0 график функции y = f(kx)
есть зеркальное отображение графика
y = f(–kx) от оси Oy.
Care dintre aceste funcții au inversă? Pentru astfel de funcții, găsiți funcții inverse:
4.12. A) |
y = x ; |
b) y = 6 −3 x ; |
|||||
d) y = |
e) y = 2 x 3 +5; |
||||||
4.13. A) |
y = 4 x − 5 ; |
y = 9 − 2 x − x 2 ; |
|||||
y = semnul x ; |
y =1 + log(x + 2) ; |
||||||
y = 2 x 2 +1 ; |
|||||||||
x − 2 |
|||||||||
la x< 0 |
|||||||||
c) y = |
−x |
||||||||
pentru x ≥ 0 |
|||||||||
Aflați care dintre aceste funcții sunt monotone, care sunt strict monotone și care sunt limitate:
4.14. A) |
f (x) = c, c R ; |
b) f (x) = cos 2 x; |
c) f (x) = arctan x; |
|||||||||||||
d) f (x) = e 2 x; |
e) f (x) = −x 2 + 2 x; |
e) f (x) = |
||||||||||||||
2x+5 |
||||||||||||||||
y = ctg7 x . |
||||||||||||||||
4.15. A) |
f(x) = 3− x |
b) f(x) = |
f(x)= |
x+3 |
||||||||||||
x+6 |
||||||||||||||||
X< 0, |
3x+5 |
|||||||||||||||
d) f (x) = 3 x 3 − x; |
− 10 la |
f(x)= |
||||||||||||||
e) f (x) = |
x 2 la |
x ≥ 0; |
x+1 |
|||||||||||||
f (x) = tan(sin x). |
||||||||||||||||
4.2. Funcții elementare. Convertirea graficelor de funcții
Reamintim că graficul funcției f (x) în sistemul de coordonate cartezian dreptunghiular Oxy este mulțimea tuturor punctelor planului cu coordonatele (x, f (x)).
Adesea, graficul funcției y = f (x) poate fi construit folosind transformări (deplasare, întindere) ale graficului unei funcții deja cunoscute.

În special, din graficul funcției y = f (x) se obține graficul funcției:
1) y = f (x) + a – deplasare de-a lungul axei Oy cu unități a (în sus dacă a > 0 și în jos dacă a< 0 ;
2) y = f (x −b) – deplasare de-a lungul axei Ox cu b unități (la dreapta, dacă b > 0,
și a plecat dacă b< 0 ;
3) y = kf (x) – întinderea de-a lungul axei Oy de k ori;
4) y = f (mx) – compresie de-a lungul axei Ox de m ori;
5) y = − f (x) – reflexie simetrică față de axa Ox;
6) y = f (−x) – reflexie simetrică față de axa Oy;
7) y = f (x), după cum urmează: o parte a graficului situată nu
sub axa Ox, rămâne neschimbată, iar partea „de jos” a graficului este reflectată simetric în raport cu axa Ox;
8) y = f (x), după cum urmează: partea dreaptă a graficului (pentru x ≥ 0)
rămâne neschimbat, iar în locul celui „stânga” se construiește o reflectare simetrică a celui „dreapta” în raport cu axa Oy.
Principalele funcții elementare se numesc:
1) funcția constantă y = c;
2) funcția de putere y = x α , α R ;
3) funcția exponențială y = a x, a ≠ 0, a ≠1;
4) logaritmică funcția y = log a x , a > 0, a ≠ 1 ;
5) trigonometric funcții y = sin x, y = cos x, y = tan x,
y = ctg x, y = sec x (unde sec x = cos 1 x), y = cosec x (unde cosec x = sin 1 x);
6) funcții trigonometrice inverse y = arcsin x, y = arccos x, y = arctan x, y = arcctg x.
Funcții elementare sunt numite funcții obținute din funcții elementare de bază folosind un număr finit de operații aritmetice (+, −, ÷) și compoziții (adică formarea de funcții complexe f g).

Exemplul 4.6. Reprezentați grafic funcția
1) y = x 2 + 6 x + 7 ; 2) y = −2sin 4 x .
Rezolvare: 1) prin selectarea unui pătrat complet, funcția se transformă în forma y = (x +3) 2 − 2, prin urmare graficul acestei funcții poate fi obținut din graficul funcției y = x 2. Este suficient să deplasăm mai întâi parabola y = x 2 cu trei unități la stânga (obținem un grafic al funcției y = (x +3) 2), și apoi două unități în jos (Fig. 4.1);
standard |
sinusoid |
y = sinx |
de patru ori de-a lungul axei |
Bou, |
|||||||
obţinem un grafic al funcţiei y = sin 4 x (Fig. 4.2). |
|||||||||||
y=sin4x |
|||||||||||
y=sin x |
|||||||||||
Prin întinderea de două ori a graficului rezultat de-a lungul axei Oy, obținem un grafic al funcției y = 2sin 4 x (Fig. 4.3). Rămâne să afișați ultimul grafic relativ la axa Ox. Rezultatul va fi graficul dorit (vezi Fig. 4.3).

y=2sin4x |
|||||||
y=– 2sin4 x
Probleme de rezolvat independent
Construiți grafice ale următoarelor funcții pe baza graficelor funcțiilor elementare de bază:
4.16. a) y = x 2 −6 x +11 ;
4.17. a) y = −2sin(x −π ) ;
4.18. a) y = − 4 x −1 ;
4.19. a) y = log 2 (−x);
4.20. a) y = x +5 ;
4.21. a) y = tg x ;
4.22. a) y = semnul x;
4.23. a) y = x x + + 4 2 ;
y = 3 − 2 x − x 2 .
y = 2cos 2 x .
Funcțiile elementare de bază în forma lor pură fără transformare sunt rare, așa că cel mai adesea trebuie să lucrați cu funcții elementare care au fost obținute din cele principale prin adăugarea de constante și coeficienți. Astfel de grafice sunt construite folosind transformări geometrice ale funcțiilor elementare date.
Să luăm în considerare exemplul unei funcții pătratice de forma y = - 1 3 x + 2 3 2 + 2, al cărei grafic este parabola y = x 2, care este comprimată de trei ori față de Oy și simetrică față de la Ox și deplasat cu 2 3 de-a lungul Ox la dreapta, în sus cu 2 unități de-a lungul Oy. Pe o linie de coordonate arată astfel:
Yandex.RTB R-A-339285-1
Transformări geometrice ale graficului unei funcții
Aplicând transformări geometrice ale unui grafic dat, aflăm că graficul este reprezentat de o funcție de forma ± k 1 · f (± k 2 · (x + a)) + b, când k 1 > 0, k 2 > 0 sunt coeficienți de compresie la 0< k 1 < 1 , 0 < k 2 < 1 или растяжения при k 1 >1, k 2 > 1 de-a lungul O y și O x. Semnul din fața coeficienților k 1 și k 2 indică o afișare simetrică a graficului în raport cu axele, a și b îl deplasează de-a lungul O x și de-a lungul O y.
Definiția 1
Există 3 tipuri transformări geometrice ale graficului:
- Scalare de-a lungul O x și O y. Aceasta este influențată de coeficienții k 1 și k 2 cu condiția ca aceștia să nu fie egali cu 1 când 0< k 1 < 1 , 0 < k 2 < 1 , то график сжимается по О у, а растягивается по О х, когда k 1 >1, k 2 > 1, apoi graficul este întins de-a lungul O y și comprimat de-a lungul O x.
- Afișare simetrică față de axele de coordonate. Dacă există semnul „-” în fața lui k 1, simetria este relativă la O x, iar în fața lui k 2 este relativă la O y. Dacă „-” lipsește, atunci elementul este omis la rezolvare;
- Transfer paralel (deplasare) de-a lungul O x și O y. Transformarea se realizează dacă există coeficienți a și b inegali cu 0. Dacă a este pozitiv, graficul este deplasat la stânga cu | a | unități, dacă a este negativ, atunci la dreapta la aceeași distanță. Valoarea b determină mișcarea de-a lungul axei O y, ceea ce înseamnă că atunci când b este pozitiv, funcția se mișcă în sus, iar când b este negativ, se mișcă în jos.
Să ne uităm la soluții folosind exemple, începând cu o funcție de putere.
Exemplul 1
Transformați y = x 2 3 și reprezentați grafic funcția y = - 1 2 · 8 x - 4 2 3 + 3 .
Soluţie
Să reprezentăm funcțiile astfel:
y = - 1 2 8 x - 4 2 3 + 3 = - 1 2 8 x - 1 2 2 3 + 3 = - 2 x - 1 2 2 3 + 3
Unde k 1 = 2, merită să acordați atenție prezenței „-”, a = - 1 2, b = 3. De aici obținem că transformările geometrice sunt efectuate prin întinderea de-a lungul O y de două ori, afișată simetric față de O x, deplasată la dreapta cu 1 2 și în sus cu 3 unități.
Dacă descriem funcția de putere inițială, obținem asta

când este întins de două ori de-a lungul O y avem asta

Maparea, simetrică față de O x, are forma

și deplasați-vă la dreapta cu 1 2

o mișcare de 3 unități în sus arată ca

Să ne uităm la transformările funcțiilor exponențiale folosind exemple.
Exemplul 2
Construiți un grafic al funcției exponențiale y = - 1 2 1 2 (2 - x) + 8.
Soluţie.
Să transformăm funcția pe baza proprietăților unei funcții de putere. Atunci obținem asta
y = - 1 2 1 2 (2 - x) + 8 = - 1 2 - 1 2 x + 1 + 8 = - 1 2 1 2 - 1 2 x + 8
Din aceasta putem vedea că obținem un lanț de transformări y = 1 2 x:
y = 1 2 x → y = 1 2 1 2 x → y = 1 2 1 2 1 2 x → → y = - 1 2 1 2 1 2 x → y = - 1 2 1 2 - 1 2 x → → y = - 1 2 1 2 - 1 2 x + 8
Constatăm că funcția exponențială originală are forma

Strângerea de două ori de-a lungul O y dă

Întinderea de-a lungul O x

Maparea simetrică în raport cu O x
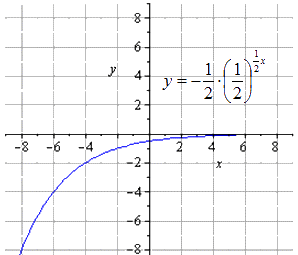
Maparea este simetrică în raport cu O y

Mutați în sus cu 8 unități

Să luăm în considerare soluția folosind exemplul unei funcții logaritmice y = ln (x).
Exemplul 3
Construiți funcția y = ln e 2 · - 1 2 x 3 folosind transformarea y = ln (x) .
Soluţie
Pentru a rezolva este necesar să folosim proprietățile logaritmului, atunci obținem:
y = ln e 2 · - 1 2 x 3 = ln (e 2) + ln - 1 2 x 1 3 = 1 3 ln - 1 2 x + 2
Transformările unei funcții logaritmice arată astfel:
y = ln (x) → y = 1 3 ln (x) → y = 1 3 ln 1 2 x → → y = 1 3 ln - 1 2 x → y = 1 3 ln - 1 2 x + 2
Să diagramăm funcția logaritmică inițială

Comprimăm sistemul conform O y

Ne întindem de-a lungul O x

Efectuăm o mapare în raport cu O y

Trecem cu 2 unități, obținem

Pentru a transforma graficele unei funcții trigonometrice, este necesar să se potrivească schemei soluții de forma ± k 1 · f (± k 2 · (x + a)) + b. Este necesar ca k 2 să fie egal cu T k 2 . De aici obținem acel 0< k 2 < 1 дает понять, что график функции увеличивает период по О х, при k 1 уменьшает его. От коэффициента k 1 зависит амплитуда колебаний синусоиды и косинусоиды.
Să ne uităm la exemple de rezolvare a problemelor cu transformări y = sin x.
Exemplul 4
Construiți un grafic al lui y = - 3 sin 1 2 x - 3 2 - 2 folosind transformări ale funcției y=sinx.
Soluţie
Este necesar să se reducă funcția la forma ± k 1 · f ± k 2 · x + a + b. Pentru aceasta:
y = - 3 sin 1 2 x - 3 2 - 2 = - 3 sin 1 2 (x - 3) - 2
Se poate observa că k 1 = 3, k 2 = 1 2, a = - 3, b = - 2. Deoarece există un „-” înainte de k 1, dar nu înainte de k 2, atunci obținem un lanț de transformări de forma:
y = sin (x) → y = 3 sin (x) → y = 3 sin 1 2 x → y = - 3 sin 1 2 x → → y = - 3 sin 1 2 x - 3 → y = - 3 sin 1 2 (x - 3) - 2
Transformare detaliată a undei sinusoidale. Când trasăm sinusoida originală y = sin (x), aflăm că cea mai mică perioadă pozitivă este considerată a fi T = 2 π. Aflarea maximului în punctele π 2 + 2 π · k; 1, iar minimul - - π 2 + 2 π · k; - 1, k ∈ Z.

O y este întins de trei ori, ceea ce înseamnă că creșterea amplitudinii oscilațiilor va crește de 3 ori. T = 2 π este cea mai mică perioadă pozitivă. Maximele merg la π 2 + 2 π · k; 3, k ∈ Z, minime - - π 2 + 2 π · k; - 3, k ∈ Z.
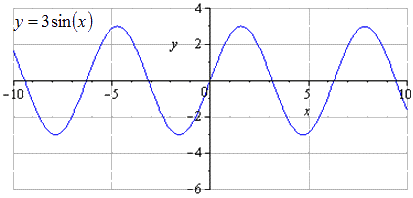
Când se întinde de-a lungul O x la jumătate, constatăm că cea mai mică perioadă pozitivă crește de 2 ori și este egală cu T = 2 π k 2 = 4 π. Maximele merg la π + 4 π · k; 3, k ∈ Z, minime – în - π + 4 π · k; - 3, k ∈ Z.

Imaginea este produsă simetric în raport cu O x. Cea mai mică perioadă pozitivă în acest caz nu se modifică și este egală cu T = 2 π k 2 = 4 π. Tranziția maximă arată ca - π + 4 π · k; 3, k ∈ Z, iar minimul este π + 4 π · k; - 3, k ∈ Z.

Graficul este deplasat în jos cu 2 unități. Perioada minimă comună nu se modifică. Găsirea maximelor cu trecerea la puncte - π + 3 + 4 π · k; 1, k ∈ Z, minime - π + 3 + 4 π · k; - 5 , k ∈ Z .

În această etapă, graficul funcției trigonometrice este considerat transformat.
Să considerăm o transformare detaliată a funcției y = cos x.
Exemplul 5
Construiți un grafic al funcției y = 3 2 cos 2 - 2 x + 1 folosind o transformare a funcției de forma y = cos x.
Soluţie
Conform algoritmului, este necesar să se reducă funcția dată la forma ± k 1 · f ± k 2 · x + a + b. Atunci obținem asta
y = 3 2 cos 2 - 2 x + 1 = 3 2 cos (- 2 (x - 1)) + 1
Din condiție este clar că k 1 = 3 2, k 2 = 2, a = - 1, b = 1, unde k 2 are „-”, iar înainte de k 1 este absent.
Din aceasta vedem că obținem un grafic al unei funcții trigonometrice de forma:
y = cos (x) → y = 3 2 cos (x) → y = 3 2 cos (2 x) → y = 3 2 cos (- 2 x) → → y = 3 2 cos (- 2 (x - 1) )) → y = 3 2 cos - 2 (x - 1) + 1
Transformare cosinus pas cu pas cu ilustrare grafică.
Având în vedere graficul y = cos(x), este clar că cea mai scurtă perioadă totală este T = 2π. Găsirea maximelor în 2 π · k ; 1, k ∈ Z, și există π + 2 π · k minime; - 1, k ∈ Z.
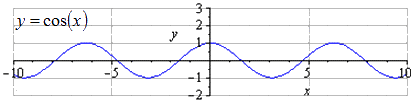
Când este întins de-a lungul Oy de 3 2 ori, amplitudinea oscilațiilor crește de 3 2 ori. T = 2 π este cea mai mică perioadă pozitivă. Găsirea maximelor în 2 π · k ; 3 2, k ∈ Z, minime în π + 2 π · k; - 3 2 , k ∈ Z .

Când este comprimată de-a lungul O x la jumătate, aflăm că cea mai mică perioadă pozitivă este numărul T = 2 π k 2 = π. Maximele sunt transferate la π · k ; 3 2 , k ∈ Z , minime - π 2 + π · k ; - 3 2 , k ∈ Z .

Harta simetrica fata de Oy. Deoarece graficul este impar, nu se va schimba.

Când graficul este deplasat cu 1. Nu există modificări în cea mai mică perioadă pozitivă T = π. Găsirea maximelor în π · k + 1 ; 3 2, k ∈ Z, minime - π 2 + 1 + π · k; - 3 2 , k ∈ Z .

Când este deplasată cu 1, cea mai mică perioadă pozitivă este egală cu T = π și nu se modifică. Găsirea maximelor în π · k + 1 ; 5 2, k ∈ Z, minime în π 2 + 1 + π · k; - 1 2 , k ∈ Z .

Transformarea funcției cosinus este completă.
Să luăm în considerare transformările folosind exemplul y = t g x.
Exemplul 6
Construiți un grafic al funcției y = - 1 2 t g π 3 - 2 3 x + π 3 folosind transformări ale funcției y = t g (x) .
Soluţie
Pentru început, este necesar să reducem funcția dată la forma ± k 1 · f ± k 2 · x + a + b, după care obținem că
y = - 1 2 t g π 3 - 2 3 x + π 3 = - 1 2 t g - 2 3 x - π 2 + π 3
Este clar că k 1 = 1 2, k 2 = 2 3, a = - π 2, b = π 3, iar în fața coeficienților k 1 și k 2 există un „-”. Aceasta înseamnă că după transformarea tangentelor obținem
y = t g (x) → y = 1 2 t g (x) → y = 1 2 t g 2 3 x → y = - 1 2 t g 2 3 x → → y = - 1 2 t g - 2 3 x → y = - 1 2 t g - 2 3 x - π 2 → → y = - 1 2 t g - 2 3 x - π 2 + π 3
Transformarea pas cu pas a tangentelor cu reprezentare grafică.
Avem că graficul original este y = t g (x) . Modificarea perioadei pozitive este egală cu T = π. Domeniul de definiție este considerat a fi - π 2 + π · k ; π 2 + π · k, k ∈ Z.

Îl comprimăm de 2 ori de-a lungul Oy. T = π este considerată cea mai mică perioadă pozitivă, unde domeniul de definiție are forma - π 2 + π · k; π 2 + π · k, k ∈ Z.

Întindeți de-a lungul O x 3 2 ori. Să calculăm cea mai mică perioadă pozitivă și a fost egală cu T = π k 2 = 3 2 π . Și domeniul de definire al funcției cu coordonate este 3 π 4 + 3 2 π · k; 3 π 4 + 3 2 π · k, k ∈ Z, se modifică doar domeniul de definiție.

Simetria merge pe partea O x. Perioada nu se va schimba în acest moment.

Este necesar să afișați axele de coordonate simetric. Domeniul de definiție în acest caz este neschimbat. Programul coincide cu cel precedent. Aceasta sugerează că funcția tangentă este impară. Dacă atribuim o mapare simetrică a O x și O y unei funcții impare, atunci o transformăm în funcția originală.
Soluţie
Mai întâi trebuie să treceți de la arccosinus la arcsinus folosind inverse funcții trigonometrice a r c sin x + a r c o cos x = π 2 . Aceasta înseamnă că obținem că a r c sin x = π 2 - a r c cos x.
Se poate observa că y = a r c cos x → y = - a r c cos x → y = - a r c cos x + π 2.
Transformarea arccosinusului pas cu pas și reprezentarea grafică.
Program dat de condiție

Efectuăm o mapare în raport cu O x
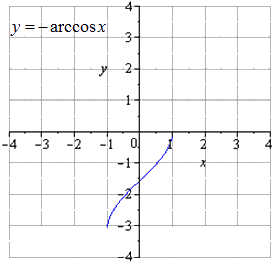
Ne deplasăm în sus cu π 2.
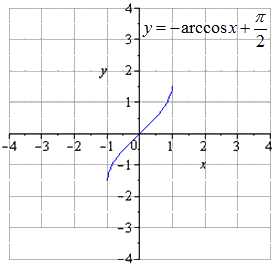
Astfel, se realizează trecerea de la arccosinus la cosinus. Este necesar să se efectueze transformări geometrice ale arcsinusului și ale graficului acestuia.
Se poate observa că k 1 = 2, k 2 = 1 3, a = - 1, b = 0, unde semnul „-” lipsește pentru k 1 și k 2.
De aici rezultă că transformarea y = a r c sin x ia forma:
y = a r c sin (x) → y = 2 a r c sin (x) → → y = 2 a r c sin 1 3 x → y = 2 a r c sin 1 3 (x - 1)
Transformarea pas cu pas a graficului arcsinus și reprezentarea grafică.
Graficul y = a r c sin x are un domeniu de forma x ∈ - 1 ; 1, atunci intervalul y ∈ - π 2; π 2 aparține domeniului de valori.

Este necesar să-l întindeți de două ori de-a lungul O y, iar domeniul de definiție va rămâne neschimbat x ∈ - 1; 1 și intervalul de valori y ∈ - π; π.

Întindere conform structurii Ox. Domeniul de definiție x ∈ - 3 este extins; 3, dar intervalul de valori rămâne neschimbat y ∈ - π; π.
